Complex numbers

Introduction

The square root of $-1$

The field of real numbers is quite powerful (and complex). Still, there are simple algebraic equations with no solutions. In particular,

$$x^2+1=0.$$

What if we define $\mathbb{i}$ as the solution to this equation? That is, $\mathbb{i}$ is a number such that

$$\mathbb{i}^2+1=0.$$

We can then use this definition to find out how $\mathbb{i}$ behaves when interacting with other numbers. First, by rearranging, we find that

$$\mathbb{i}^2=-1.$$

For this reason, we sometimes repersent $\mathbb{i}$ with $\sqrt{-1}$. Other notations include $i$ and $j$, with the latter being common in electrical engineering (to avoid confusion with the symbol $i$ used for current.) We will use $i$ and $\mathbb{i}$ interchangeably. The number $\mathbb{i}$ is called the imaginary unit, but the way we arrived at it is similar to defining negative numbers, e.g., as the solution to $x+1=0$. So in a sense, $\mathbb{i}$ is not less “real” than $-1$.

If $\mathbb{i}$ is a solution then $−\mathbb{i}$ must be another solution: $(−\mathbb{i})^2=(-\mathbb{i})\times(-\mathbb{i})=\mathbb{i}\times \mathbb{i} = -1$.

What is $1/\mathbb{i}$? In other words, what is $x$ such that $\mathbb{i}\times x = 1$?

\[\mathbb{i}\times x = 1 \Rightarrow \mathbb{i}\times \mathbb{i}\times x = \mathbb{i}\Rightarrow -1\times x = \mathbb{i} \Rightarrow x = -\mathbb{i}.\]

Definition:
The set of complex numbers is defined as
$$\mathbb{C}=\{a+b\mathbb{i}: a,b \in \mathbb{R}\}$$ with the following operations and inverses:
 Addition: \( (a+b\mathbb{i})+(c+d\mathbb{i})=a+c+\mathbb{i}(b+d) \)
 Multiplication: \( (a+b\mathbb{i})(c+d\mathbb{i})=ac+ad\mathbb{i}+bc\mathbb{i}+bd\mathbb{i}^2=ac−bd+(ad+bc)\mathbb{i} \)
 Additive inverse: \( −(a+b\mathbb{i})=(−a)+(−b)\mathbb{i}  \) 
 Multiplicative inverse: \( \frac{1}{(a+b\mathbb{i})}=\frac{1}{(a+b\mathbb{i})}\frac{(a−b\mathbb{i})}{(a−b\mathbb{i})}=\frac{(a−b\mathbb{i})}{(a^2+b^2 )}=\frac{a}{(a^2+b^2 )}−\frac{b}{(a^2+b^2)} \mathbb{i} \)

Numbers: Summary

Recall that we started with natural numbers and gradually built up to construct real numbers numbers. Now we have also added complex numbers.

Set	Symbol	Elements	Operations	What’s missing?
Natural numbers	$\mathbb N$	0,1,2,…	$+ \times$	Solve $x+3=0$
Integers	$\mathbb Z$	…,-2,-1,0,1,2,…	$+\times - /$	Solve $3x+1=0$
Rationals	$\mathbb Q$	$0,\pm 1,\pm\frac12,...$	$+\times -/$	Solve $x^2=2$ Perimeter of unit circle
Reals	$\mathbb R$	Limits of converging sequences in $\mathbb Q$	$+\times -/$	Solve $x^2+1=1$
Complex numbers	$\mathbb C$	$\{a+b\mathbb{i}: a,b\in\mathbb R\}$	$+\times -/$

Complex numbers are said to be complete (contain the limits of all converging sequences) and algebraically closed (all polynomials have roots). The latter property is stated in the fundamental theorem of algebra, discussed below.

Two Representations

Geometric representation

Real numbers can be represented on the (1-dimensional) real line. For example, $r=2.2$ is shown below.

Complex numbers are represented on the (2-dimentional) complex plane. Specifically, $z=x+iy, x,y\in \mathbb R$ is given by the pont $(x,y)$. In the graph below, you can drag the point $z$ to see this representation in action.

For a complex number $z = a + ib$.

Real part: $Re(z) = a$
Imaginary part: $Im(z) = b$
Magnitude: distance from origin, $\left\vert z \right\vert = \sqrt{a^{2} + b^{2}}$
Phase: angle (counterclockwise) from the real line $\angle z = \tan^{- 1}\frac{b}{a}$

Plot the following numbers in the complex plane: $z_{1} = 1$, $z_{2} = i$, $z_{3} = 3 + 2i$, $z_{4} = z_{2} + z_{3}$, $z_{5} = \frac{1}{z_{3}}$

What do we get of we multiply $z = a + ib$ by $i$? Show on the complex plane.

Show the powers of $i$: $i$, $i^{2},i^{3},\ldots$ on the complex plane.

Complex exponentiation

What is $a^{ix}$ when $a,x$ are real?

Let’s start with $e^{ix}$. One way to extend real functions to complex numbers is to define them based on series:

\begin{align*} e^{x} &= 1 + x + \frac{x^{2}}{2} + \frac{x^{3}}{3!} + \frac{x^{4}}{4!} + \frac{x^{5}}{5!} + \ldots\\ \cos x &= 1 - \frac{x^{2}}{2} + \frac{x^{4}}{4!} - \dotsm\\ \sin x &= x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \dotsm \end{align*}

Extending the first series to imaginary numbers, we find

\begin{align*} e^{ix} &= 1 + ix - \frac{x^{2}}{2} - i\frac{x^{3}}{3!} + \frac{x^{4}}{4!} + i\frac{x^{5}}{5!} + \dotsm\\ &= \left(1 - \frac{x^{2}}{2} + \frac{x^{4}}{4!} +\dotsm\right) + \left(ix - i\frac{x^{3}}{3!} + i\frac{x^{5}}{5!}+\dotsm\right)\\ &= \cos x + i \sin x. \end{align*}

So, we can write $e^{ix}$ in terms of $\cos x$ and $\sin x$. This is called Euler’s equation. Here is a visual proof.

 Euler's equation:
$$e^{ix} = \cos x + i \sin x.$$

Find $\sin\left( a + b \right)$ and $\cos\left( a + b \right)$ in terms of $\sin a,\sin b,\cos a,\cos b$ using Euler's equation. Hint: write $e^{i(a+b)}$ in two different ways and compare terms.

Credit: xkcd

Given the above transformation, we can also represent complex numbers as $z = {re}^{i\theta} = r \left( \cos\theta + i\sin\theta \right)$.

Real parts: $Re\left( z \right) = r\cos\theta$
Imaginary part: $Im\left( z \right) = r\sin\theta$.
Magnitude: $\left\vert z \right\vert = \sqrt{r^{2}\left( \cos\theta \right)^{2} + r^{2}\left( \sin\theta \right)^{2}} = r$
Phase: $\angle z = \tan^{- 1}\frac{\sin\theta}{\cos\theta} = \theta$.

Note that $e^{i\theta} = e^{i(\theta+2\pi)} = e^{i2\pi k+i\theta}$ for any integer $k$.

Find the real and imaginary parts of $e^{i\pi}$.

Cartesian vs Polar

We can represent a complex number $z$ in terms of:

real and imaginary parts: $z = a + ib$ (Cartesian)
magnitude and phase: $z = re^{i\theta}$ (Polar)

And one can convert it from one representation to the other:

$a = r\cos\theta,b = r\sin\theta$
$r = \sqrt{a^{2} + b^{2}},\theta = \tan^{- 1}\frac{b}{a}$

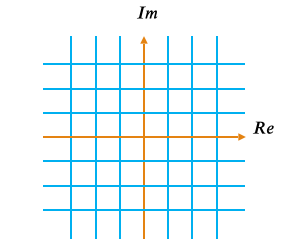
Related to these representations are two coordinate systems


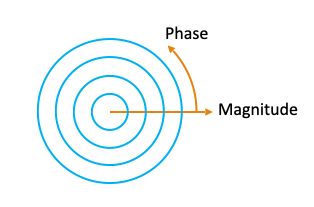Cartesian: (real part, imaginary part)	Polar: (magnitude, phase)

Note: We refer to $re^{i\theta}$ as the polar representation, even if we don’t necessarily use the polar axis shown on the right.

Polar representation

Examples: $z_{1} = 1.5e^{i\pi/6}$, $z_{2} = 2e^{- i2\pi/6}$, $z_{3} = z_{1}z_{2}$, $z_{4} = 1/z_{2}$

Arithmetic in the complex plane

The right representation simplifies computation.

Cartesian:

Addition/subtraction: $a + ib + c + id = \left( a + c \right) + i(b + d)$

Polar:

Multiplication: $re^{i\theta} \times \rho e^{i\phi} = r\rho e^{i\left( \theta + \phi \right)}$
Inverse: $\frac{1}{r e^{i\theta}} = \frac1r e ^{-i\theta}$
Division: $\frac{\rho e^{i\phi}}{r e^{i\theta}} = \frac{\rho}{\phi}e^{-i(\phi-\theta)} $
Power (to the power of $n$): ${(re^{i\theta})}^n = r^n e^{i n\theta}$

Signals in the complex plane

We can represent real signals on a two-dimensional graph. How about complex signals?

Complex signals can be viewed as a path on the complex plain, or rather as a point moving along a path on the complex plain. For example, the complex signal $z(t)=e^{i2\pi t}$ can be shown as a path on the complex plane below.

Signals of the form $e^{i\omega t}$ are called complex exponentials and are very important!

\[Re(e^{i2\pi t}) = \cos(2\pi t),\qquad Im(e^{i2\pi t}) = \sin(2\pi t).\]

Let $f\left( t \right) = t$. Represent $f\left( t \right)e^{i2\pi t}$ as a path on the complex plane. You may use some easy to compute points like $t=0, \frac12, \frac14, \ldots$ to approximately determine the path.

Fundamental theorem of algebra

For a polynomial $f(x)$ of $x$, any value of $x$ that satisfies $f(x)=0$ is called a root. For example, $x=1$ is a root of $x^2+x-2$ since $1^2+1-2=0$.

If $x=x_0$ is a root of $f(x)$, then $(x-x_0)$ is a factor of $f(x)$. That is, we can write $f(x)$ as a product of $x-x_0$ and some other polynomial. In other words, a polynomial $g(x)$ exists such that $f(x) = (x-x_0)g(x)$. In our example, from the previous paragraph, we have $x^2+x-2=(x-1)(x+2)$.

On the other hand, if $x-x_0$ is a factor of $f(x)$, then $x_0$ is a root of $f(x)$ since $f(x_0)=0$. In our example, $x=-2$ is another root since $x+2$ is a factor.

A value $x_0$ can be the root of a polynomial multiple times, meaning that the factor $(x-x_0)$ appears multiple times. For example, since $x^4 - x^3 - 3x^2 + 5x - 2=(x-1)^3(x+2)$, the roots are $1,1,1,-2$. We say that this polynomial has 4 roots, 1 of which has multiplicity 3.

In the set of real numbers, not all polynomials have roots. An obvious example is $x^2+1$. But the situation is different for complex numbers.

The fundamental theorem of algebra:
 Every non-constant polynomial has a complex root.
 Every polynomial of degree \(n\) can be written as a product of \(n\) first-degree polynomials and has precisely \(n\) roots.

The following two identities are sometimes useful for finding the roots:

\begin{align*} a^2-b^2 &= (a-b) (a+b)\\ a^2+b^2 &= (a-\mathbb{i}b) (a+\mathbb{i}b) \end{align*}

For example:

\begin{align*} x^2+1 &= (x-\mathbb{i})(x+\mathbb{i})\Rightarrow roots = -\mathbb{i},\mathbb{i}\\ x^{5} - x^{3} &= x^3(x^2-1)=x^{3}\left( x - 1 \right)\left( x + 1 \right) \Rightarrow roots = 0,0,0,1, - 1\\ x^{2} + 5 &= \left( x - {\mathbb{i}}\sqrt{5} \right)\left( x + {\mathbb{i}}\sqrt{5} \right) \Rightarrow roots = {\mathbb{i}}\sqrt{5}, - {\mathbb{i}}\sqrt{5}\\ x^{3} - 1 &= \left( x - 1 \right)\left( x^{2} + x + 1 \right) = \left( x - 1 \right)\left( x^{2} + x + \frac{1}{4} + \frac{3}{4} \right) = \left( x - 1 \right)\left( \left( x + \frac{1}{2} \right)^{2} + \frac{3}{4} \right)\\ &= (x - 1)\left( x + \frac{1}{2} + \frac{ \mathbb{i}\sqrt{3} }{2} \right)\left( x + \frac{1}{2} - \frac{\mathbb{i}\sqrt{3}}{2} \right)\Rightarrow roots = 1,-\frac{1}{2} - \frac{\mathbb{i}\sqrt{3}}{2},-\frac{1}{2} - \frac{\mathbb{i}\sqrt{3}}{2} \end{align*}

Conjugate

The conjugate of a complex number $z = a + ib$ is $z^{\ast} = a - ib$. In polar form, the conjugate of $z = re^{i\theta}$ is $z^{\ast} = re^{- i\theta}$.

If a real polynomial has a complex root $w$, then $w^{\ast}$ is also a root.

Example: $x^{2} - 2x + 2 = 0 \Rightarrow (x^2 - 2x + 1) = -1 \Rightarrow (x - 1)^2 = -1$. Then the roots are $1 \pm i$.

Roots of unity

What are the solutions to $z^{3} = 1$?

Recall: $re^{i\theta} = re^{i\left( 2\pi k + \theta \right)}$
$z^{3} = 1 \Rightarrow \left( re^{i\theta} \right)^{3} = 1 \Rightarrow r^{3}e^{i3\theta} = 1e^{i0} \Rightarrow \begin{cases} r = 1 \\ 3\theta = 2\pi k \\ \end{cases} \Rightarrow \begin{cases} r = 1 \\ \theta = \frac{2\pi k}{3} \\ \end{cases} \Rightarrow \begin{cases} r = 1 \\ \theta = 0,\frac{2\pi}{3},\frac{4\pi}{3} \\ \end{cases}$

What about $z^{n} = 1$? Whare are the roots of $z^{n} = re^{i\theta}$?

Demonstration:

Set	Symbol	Elements	Operations	What’s missing?
Natural numbers	\(\mathbb N\)	0,1,2,…	\(+ \times\)	Solve \(x+3=0\)
Integers	\(\mathbb Z\)	…,-2,-1,0,1,2,…	\(+\times - /\)	Solve \(3x+1=0\)
Rationals	\(\mathbb Q\)	\(0,\pm 1,\pm\frac12,...\)	\(+\times -/\)	Solve \(x^2=2\) Perimeter of unit circle
Reals	\(\mathbb R\)	Limits of converging sequences in \(\mathbb Q\)	\(+\times -/\)	Solve \(x^2+1=1\)
Complex numbers	\(\mathbb C\)	\(\{a+b\mathbb{i}: a,b\in\mathbb R\}\)	\(+\times -/\)