Matrices and fundamental spaces

Matrices, the basics

What is a Matrix?

A matrix is a finite, ordered sequence of numbers arranged in a rectangle with a number of rows and columns.

Examples:

\[A = \begin{pmatrix} 3 & -1 \\ 1 & 2 \\ \end{pmatrix},\qquad B = \begin{pmatrix} -1 & 1 \\ 7 & 4 \\ 0 & 3 \\ \end{pmatrix}.\]

To refer the element in row $i$ and column $j$ of $A$, we write $A_{ij}$. For example, above, $A_{12}=-1.$

The dimension of a matrix is written as $m\times n$, where $m$ is the number of rows and $n$ is the number of columns. We write $A_{m\times n}$ to denote a matrix of dimension $m\times n$.

Addition: Matrices can be added and multiplied together. The addition of two matrices with the same dimensions is obtained by adding the elements in the same positions, as shown below. Multiplication is discussed later in detail.

\[\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix} + \begin{pmatrix}7&8&9\\10&11&12\end{pmatrix} = \begin{pmatrix}8&10&12\\14&16&18\end{pmatrix}.\]

Transposition: We can transpose a matrix by mirroring it with respect to the diagonal:

\[\begin{pmatrix} 2 & -3 \\ -1 & 4 \\ 1 & 0 \\ \end{pmatrix}^{T} = \begin{pmatrix} 2 & -1 & 1 \\ -3 & 4 & 0 \\ \end{pmatrix}\]

Vectors as matrices: Vectors are special cases of matrices, where either one row or one column:

• Column vector: elements arranged in a single column; a D-dimensional column vector is a $D\times1$ matrix. These are more common and the default format for vectors.
• Row vector: elements arranged in a single row; a D-dimensional row vector is a $1\times D$ matrix.

We use the notation $v = \left( v_{1},v_{2},\ldots,v_{n} \right)$ for both row and column vectors. If we want to be precise, to write a column vector as a row vector, we can write $v^T=\left( v_{1},v_{2},\ldots,v_{n} \right)$. If $v$ is a column vector, $v^T$ is a row vector and vice versa.

It is usually helpful to think of a matrix as a collection of (usually column) vectors.

\[\begin{pmatrix} \color{blue}{ - 1} & \color{blue}{1} \\ \color{brown}{0} & \color{brown}{3} \\ \color{green}{2 }& \color{green}{- 2} \\ \end{pmatrix},\qquad \begin{pmatrix} \color{blue}{ -5 }& \color{brown}{-6} & \color{green}{-4 }\\ \color{blue}{5 }& \color{brown}{8 }& \color{green}{7} \\ \color{blue}{ -1 }& \color{brown}{0} & \color{green}{1 }\\ \end{pmatrix}.\]

Matrix-vector multiplication

We can multiply a vector $x$ and a matrix $A$ in two different ways: \(Ax\) and \(xA\)

• For $Ax$, the number of columns of $A$ must be the same as the number of elements of $x$. $x$ must be a column vector. The result is the linear combination of the columns of $A$, where the coefficients are the elements of $x$:

\[\begin{pmatrix} \color{blue}{1} & \color{brown}{-1} \\ \color{blue}{3} & \color{brown}{-4} \\ \color{blue}{-1} & \color{brown}{2} \\ \end{pmatrix} \begin{pmatrix} \color{blue}{2} \\ \color{brown}{1} \\ \end{pmatrix} = \color{blue}{2} \begin{pmatrix} \color{blue}{1} \\ \color{blue}{3} \\ \color{blue}{-1}\\ \end{pmatrix} + \color{brown}{1} \begin{pmatrix} \color{brown}{-1} \\ \color{brown}{-4} \\ \color{brown}{2} \\ \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 0 \\ \end{pmatrix}\]

More generally, for \(A = \begin{pmatrix} \color{blue}{a_{11}} & a_{12} & a_{13} \\ \color{blue}{a_{21}} & a_{22} & a_{23} \\ \color{blue}{a_{31}} & a_{32} & a_{33} \\ \color{blue}{a_{41}} & a_{42} & a_{43} \\ \end{pmatrix},x = \begin{pmatrix} \color{blue}{x_{1}} \\ x_{2} \\ x_{3} \\ \end{pmatrix},\) we have

\[Ax = \color{blue}{x_{1}}\begin{pmatrix} \color{blue}{a_{11}} \\ \color{blue}{a_{21}} \\ \color{blue}{a_{31}} \\ \color{blue}{a_{41}} \\ \end{pmatrix} + x_{2}\begin{pmatrix} a_{12} \\ a_{22} \\ a_{32} \\ a_{42} \\ \end{pmatrix} + x_{3}\begin{pmatrix} a_{13} \\ a_{23} \\ a_{33} \\ a_{43} \\ \end{pmatrix}= \begin{pmatrix} \color{blue}{x_{1}a_{11}} + x_{2}a_{12} + x_{3}a_{13} \\ \color{blue}{x_{1}a_{21}} + x_{2}a_{22} + x_{3}a_{23} \\ \color{blue}{x_{1}a_{31}} + x_{2}a_{32} + x_{3}a_{33} \\ \color{blue}{x_{1}a_{41}} + x_{2}a_{42} + x_{3}a_{43} \\ \end{pmatrix}\]

• For $xA$, the number of rows of $A$ must be the same as the number of elements of $x$. $x$ must be a row vector. The result is the linear combination of the rows of $A$, where the $i$-th element of $x$ is the coefficient of the $i$-th column of $A$:

\[\begin{pmatrix} \color{blue}{ - 1} & \color{brown}{1 }& \color{green}{0} \\ \end{pmatrix}\begin{pmatrix} \color{blue}{ - 1} & \color{blue}{1} \\ \color{brown}{0} & \color{brown}{3} \\ \color{green}{2 }& \color{green}{- 2} \\ \end{pmatrix} = \color{blue}{ - 1} \begin{pmatrix} \color{blue}{ - 1} & \color{blue}{1} \\ \end{pmatrix} + \color{brown}{1 } \begin{pmatrix} \color{brown}{0} & \color{brown}{3} \\ \end{pmatrix} + \color{green}{0} \begin{pmatrix} \color{green}{2 }& \color{green}{- 2} \\ \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ \end{pmatrix}\]

We can multiply a column vector $v$ by a matrix from the left by first writing it as row vector, i.e., $v^T A$.

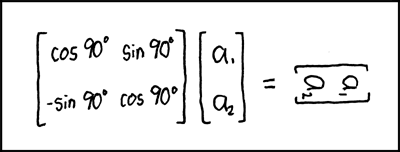
We can view matrix-vector multiplication (also vector-matrix multiplication) as a transformation, that is a function that maps vectors to vectors. The input to the transformation is $x$ and the output is $Ax$ (or $xA$). For example, a transformation may rotate each vector by 90 degrees.

Matrix-vector multiplication $Ax$ is a linear transformation:

• Scaling: $A(cx) = c(Ax)$
• Additivity: $A(x+y) = Ax + Ay$

Note: this also holds for the vector-matrix multiplication $xA$.

Matrix multiplication

We can also multiply two matrices together. In this case, the $i$-th column of the result is obtained by multiplying the $i$-th column of the second matrix by the first matrix. For example,

\[\begin{pmatrix} 2 & -3 \\ -1 & 4 \\ 1 & 0 \\ \end{pmatrix}\begin{pmatrix} \color{blue}{ -1 }&\color{brown}{ 0 }&\color{green}{ 1 }\\ \color{blue}{1 }&\color{brown}{ 2 }& \color{green}{2 }\\ \end{pmatrix} = \begin{pmatrix} \color{blue}{ -5 }& \color{brown}{-6} & \color{green}{-4 }\\ \color{blue}{5 }& \color{brown}{8 }& \color{green}{7} \\ \color{blue}{ -1 }& \color{brown}{0} & \color{green}{1 }\\ \end{pmatrix}\]

Note for example that the first column of the result is obtained by multiplying the first column of the second matrix by the first matrix:

\[\begin{pmatrix} 2 & -3 \\ -1 & 4 \\ 1 & 0 \\ \end{pmatrix}\begin{pmatrix} -1\\ 1\\ \end{pmatrix} = (-1)\begin{pmatrix} 2 \\ -1 \\ 1 \\ \end{pmatrix}+ (1) \begin{pmatrix} -3 \\ 4 \\ 0 \\ \end{pmatrix}= \begin{pmatrix} -5\\ 5\\ -1\\ \end{pmatrix}\]

We can also view matrix multiplication as follows: If $C=AB$, then $C_{ij}$ is the result of the inner product of the $i$-th row of $A$ and the $j$-th column of $B$. The number of columns of $A$ must equal the number of rows of $B$. $A_{n\times m} B_{m \times p} = C_{n \times p}$.

Note that matrix-vector multiplication can be viewed as a special case of matrix multiplication.

Properties of matrix multiplication

• Matrix multiplication is not commutative. If $AB$ and $BA$ are both defined, they may be different.
• Matrix multiplication is associative: $A(BC) = (AB)C$. Similarly, for a vector $x$, $A(Bx)=(AB)x$.
• Matrix multiplication is distributive: $A(B+C) = AB+AC$.
• Transposition: $(AB)^T = B^TA^T.$

The identity matrix

The $n \times n$ identity matrix has 1s on the diagonal and 0s elsewhere \(I_{n} = \begin{pmatrix} 1 & \ldots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \ldots & 1 \\ \end{pmatrix}\)

• Matrix multiplication has the identity property: $IA = AI = A$.

The four fundamental spaces of a matrix

There are four subspaces associated with each matrix. The column space, the row space, the null space, and the left null space. The column space and the null space are particularly important in error correction.

The row space

The row space of $A$ is the span of the rows of $A$

• linear combinations of rows of $A$
• the set of vectors obtained by $x^{T}A$ for all $x$
• we show the row space as $RS(A)$.

To represent the row space in a simple way, we can find a basis for it. We can do so as explained in the last section, where we discussed how to find a basis for a subspace. When we apply this method to rows of a matrix, adding the multiple of a row to the other is called an elementary row operation and if we find the basis in the reduced form, this form is called the reduced row-echelon form. We can then represent the row space as a set of vectors with free and dependent coordinates.

The row rank of a matrix is the dimension of its row space.

The column space

The column space of $A$ is the span of the columns of $A$

• linear combinations of columns of $A$
• the set of vectors obtained by $Ax$ for all $x$
• we show the column space as $CS(A)$.

Finding a basis for the column space is similar to row space, except that here we manipulate the columns. As an example, let us find a basis for the column space of \(A = \begin{pmatrix} 1 & 1 & 3 \\ 1 & 3 & 2 \\ 2 & 4 & 6 \\ \end{pmatrix}\)

\[A \rightarrow \begin{pmatrix} 1 & 0 & 0 \\ 1 & 2 & -1 \\ 2 & 2 & 0 \\ \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & -1 \\ 2 & 1 & 0 \\ \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 1 & 1 \\ \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \rightarrow \left\{\begin{pmatrix} a \\ b \\ c \\ \end{pmatrix} \vert a, b, c \in \mathbb{R} \right\}.\]

For example, in the first step, we have subtracted the first column from the second column and 3 times the first column from the third column. In the second step, we scaled the second column and then subtracted scaled versions of it from the other columns and so on. These are called elementary column operations.

The dimension of the column space is called the column rank.

Rank of a matrix

What is the relationship between row and column ranks? They are equal, as we saw above for

\[B = \begin{pmatrix} 1 & 1 & 3 \\ 1 & 3 & 2 \\ 2 & 4 & 5 \\ \end{pmatrix}.\]

As another example, recall that the column rank of the matrix $A$ given below is 2. Let’s find its row rank

\[A = \begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & 4 \\ 4 & 9 & 14 & 19 \\ \end{pmatrix}\] \[\begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & 4 \\ 4 & 9 & 14 & 19 \\ \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 1 & 1 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 5 & 10 & 15 \\ \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 0 & -1 & -2 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 0 & 0 \\ \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 0 & -1 & -2 \\ 0 & 1 & 2 & 3 \\ \end{pmatrix}.\]

and so the row rank of $A$ is also 2.

The null space

Let $A$ be an $m\times n$ matrix. The null space of $A$, denoted $NS(A)$, is the set of $n$-dimensional vectors $x$ satisfying $Ax=\mathbf 0$.

• The null space of any matrix, at a minimum, is a vector space containing the zero vector since $A\mathbf 0 =\mathbf 0$.
• If the row rank is smaller than the number of rows, then the dimension of the null space is larger than 0, i.e., it contains other vectors than $\mathbf 0$.

Note that elementary row operations are like adding one equation to another one and so they don’t change the set of vectors satisfying $Ax=\mathbf 0$. So to find the null space, we first write the matrix in the reduced row echelon form.

Example: the null space of

\[A = \begin{pmatrix} 1 & - 1 & 2 & 1 \\ -1 & 2 & 1 & 2 \\ 2 & 1 & 2 & - 2 \\ \end{pmatrix} \rightarrow \begin{pmatrix} 1 & - 1 & 2 & 1 \\ 0 & 1 & 3 & 3 \\ 0 & 3 & -2 & -4 \\ \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 0 & 5 & 4 \\ 0 & 1 & 3 & 3 \\ 0 & 0 & -11 & -13 \\ \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 0 & 0 & - 21/11 \\ 0 & 1 & 0 & - 6/11 \\ 0 & 0 & 1 & 13/11 \\ \end{pmatrix}\]

So the null space of $A$ is the set of solutions to

\[\begin{pmatrix} 1 & 0 & 0 & - 21/11 \\ 0 & 1 & 0 & - 6/11 \\ 0 & 0 & 1 & 13/11 \\ \end{pmatrix} \begin{pmatrix}x_1\\ x_2\\ x_3\\ x_4\end{pmatrix}=\begin{pmatrix}0\\0\\0\\0\end{pmatrix},\]

which we can write as

\[\begin{matrix} x_{1} - \frac{21}{11}x_{4} = 0 \\ x_{2} - \frac{6}{11}x_{4} = 0 \\ x_{3} + \frac{13}{11}x_{4} = 0 \\ \end{matrix}\]

This allows us to express $x_1, x_2, x_3$ in terms of $x_4$, then write out the null space vector as:

\[NS(A) = \left\{ \begin{pmatrix} \frac{21}{11}x_{4} \\ \frac{6}{11}x_{4} \\ -\frac{13}{11}x_{4} \\ x_{4} \\ \end{pmatrix} \vert x_4 \in \mathbb{R} \right\}\]

On the other hand, the row space of $A$ is given by

\[RS(A) = \left\{ \begin{pmatrix} x_1 \\ x_2\\ x_3\\ \frac{-21x_1-6x_2+13x_3}{11}\\ \end{pmatrix} \vert x_1,x_2,x_3 \in \mathbb{R} \right\}.\]

We can see the set of free and dependent coordinates complement each other in the row space and the null space. This shows the following fact:

The generator matrix

Note that in the previous example, we can write the null space of the matrix $A$ as a linear combination:

\[\begin{pmatrix} (x_{3} + x_{4})/2 \\ (x_{3} - x_{4})/2 \\ x_{3} \\ x_{4} \\ \end{pmatrix} = \begin{pmatrix} 1/2 \\ 1/2 \\ 1 \\ 0 \\ \end{pmatrix}x_{3} + \begin{pmatrix} 1/2 \\ -1/2 \\ 0 \\ 1 \\ \end{pmatrix}x_{4}\]

The null space of $A$ is the column space of the matrix

\[G = \begin{pmatrix} \begin{matrix} 1/2 \\ 1/2 \\ 1 \\ 0 \\ \end{matrix} & \begin{matrix} 1/2 \\ -1/2 \\ 0 \\ 1 \\ \end{matrix} \\ \end{pmatrix}\]

We call this the generator of the null space. That is, the null space is the set of vectors of the form \(G\begin{pmatrix} x_{1} \\ x_{2} \\ \end{pmatrix}.\)

This generator matrix is not unique. For example, we can start the row operations from the opposite side (bottom right) of the matrix:

\[\begin{pmatrix} -1 & 1 & 0 & 1 \\ 3 & 1 & -2 & -1 \\ 4 & -2 & -1 & -3 \\ \end{pmatrix} \rightarrow \begin{pmatrix} 1/3 & 1/3 & -1/3 & 0 \\ 5/3 & 5/3 & -5/3 & 0 \\ 4 & -2 & -1 & -3 \\ \end{pmatrix} \rightarrow \begin{pmatrix} 0 & 0 & 0 & 0 \\ 5/3 & 5/3 & -5/3 & 0 \\ 4 & -2 & -1 & -3 \\ \end{pmatrix} \rightarrow \\ \begin{pmatrix} 1 & 1 & -1 & 0 \\ -4/3 & 2/3 & 1/3 & 1 \\ \end{pmatrix} \rightarrow \begin{pmatrix} -1 & -1 & 1 & 0 \\ -1 & 1 & 0 & 1 \\ \end{pmatrix}\] \[\rightarrow \begin{cases} x_3 = x_1 + x_2 \\ x_4 = x_1 - x_2 \end{cases}\] \[\begin{pmatrix} x_{1} \\ x_{2} \\ x_{1} + x_{2} \\ x_{1} - x_{2} \\ \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 1 \\ 1 \\ \end{pmatrix} x_{1} + \begin{pmatrix} 0 \\ 1 \\ 1 \\ -1 \\ \end{pmatrix} x_{2} \rightarrow G = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 1 \\ 1 & -1 \\ \end{pmatrix},NS = \left\{ G\begin{pmatrix} x_{1} \\ x_{2} \\ \end{pmatrix}:x_{1},x_{2} \in {\mathbb{R}} \right\}\]

The column space and left null space

The left null space (LNS) of $A$: the set of vectors $x$ such that $x^TA = 0$

For an $m \times n$ matrix $A$, the CS and LNS contain $m$-dimensional vectors

What is the relationship between CS and LNS of $A$? $dim(CS) + dim(LNS) = m$, where dim stands for dimension.

The left null space is not useful for us in the future, so it will not be discussed in detail.

In summary

Suppose we have a matrix A with M rows and N columns. Then, we can define four vector spaces:

• Row space (RS): the span of the M rows = the set of vectors $x^{T}A$ for all $x$. This vector space contains vectors of dimension N.
• Column space (CS): the span of the N columns = the set of vectors $Ax$ for all $x$. This vector space contains vectors of dimension M.
• Null space (NS): the vector space containing all N-dimensional vectors x such that Ax = 0.
• Left null space (LNS): the vector space containing all M-dimensional vectors y such that $y^{T}A = \mathbf{0}$.

It turns out these spaces tell us a lot about the underlying linear operation performed by A. To understand why, we need to introduce a couple more definitions about vectors.

The fundamental theorem of linear algebra

Theorem: For an $m \times n$ matrix $A$:

• dim(RS) = dim(CS), called rank
• NS is orthogonal to RS
• dim(NS) + dim(RS) = n
• LNS is orthogonal to CS
• dim(LNS) + dim(CS) = m