Probability theory: foundations

Information theory is essentially a subarea of probability theory. So in the next couple of sections, we’ll learn more about probability. As is our approach in this course, we’ll go beyond what is strictly needed for understanding information theory.

What is probability theory?

Probability theory is a branch of mathematics that studies the likelihood of a random event occurring, from the roll of a die to a random bit flip on your hard drive to weather. It is the basis for statistics and information theory. In principle it is similar to geometry, calculus, …. But interpreting what results from probability theory mean in the real world is more challenging than other branches of mathematics, because it raises philosophical questions about randomness and because the results are mostly about long term averages rather than a specific event. Despite this, probability is responsible, directly or indirectly, for much of the modern information age by enabling

Data compression
Telecommunications
Data storage
Mathematical cryptography
Statistical physics

It’s also a lot of fun. It was actually motivated by games of chance (gambling). It will tell you that you shouldn’t buy lottery tickets but also how to do it right if you must. It will help you assess risk better and identify disingenuous statistics.

A brief history

Gerolamo Cardano developed the mathematical foundations of probability in the 15th century, but that work was nearly lost for 100 years. In 17th century France, Fermat and Pascal developed the theories of combinatorics and probability. Pascal even famously consulted for a French count who was wondering why he was losing money on gambling. This led to the development of modern theories including the idea of expected value. Pascal’s triangle, which we will learn about, was known much earlier in other parts of the world, including in 10th century Iran and 13th century China. But, Pascal’s derivation was unique in constructing the triangle via mathematical induction.

Laplace, in 19th century, greatly expanded the applications of probability theory. In 20th century, Kolmogorov developed the axioms of probability, the basis for modern probability theory.

What is probability?

Probability describes how likely it is for a random event to occur. For example, it can tell us how likely it is

to see a 3 or a 4 when rolling a die
to see at least 3 heads in a row if we flip a coin 5 times
for the sun to rise in the east
to successfully receive a data packet sent over a noisy wireless channel
to draw a heart from a well-shuffled deck of cards
for a hacker to be able to guess our 8-character password in 1000 tries
at least two people in our class to have the same birthday
nuclear war in the 21st century
US economy growing by more than 3% this year

: Some probability theorists do not consider the last two to be in the domain of probability theory and will be angry at you if you tell them otherwise!

Probability: the basics

Outcomes and events

Probability is described in terms of experiments, outcomes, and events.

An outcome is a single possible choice or result of a random experiment. For example, flipping a coin constitutes an experiment. The two possible outcomes are Heads and Tails. If we roll a dice, the outcomes are the numbers 1,2,…,6.
An event is a set of outcomes. For example, an even number showing when a die is rolled is an event consisting of outcomes 2, 4, and 6 and we show it as the set $\{2,4,6\}$.
The sample space is the set of all outcomes and is denoted by $\Omega$. So an event is any subset of the sample space (including the empty set $\varnothing$). For flipping a coin, the sample space is {Heads,Tails} and for rolling a die, it is $\{1,2,3,4,5,6\}$.

The table below provides more examples. We often represent each outcome by a number (or multiple numbers), even when the outcomes are not numbers. While this is not necessary, it allows us to treat all sample spaces as sets of numbers, which simplifies things. The number(s) associated with each outcome are shown brackets in the table below.

Experiment	Sample space	Example events
Cloud cover tomorrow	clear [0], mostly clear [1], partly cloudy [2], mostly cloudy [3], cloudy [4]	$\{0,1,2\}$ (a decent amount of sunshine)
A dice is rolled	1,2,3,4,5,6	$\{2,3,5\}$ (a prime number showing)
Sun goes supernova in the next 24 hrs	it does [1], it doesn’t [0]	$\{0,1\}$ (all possible outcomes)
A coin is flipped twice	two heads [(0,0)], heads then tails [(0,1)], tails then heads [(1,0)], two tails [(1,1)]	$\{(0,0),(0,1),(1,0)\}$ (at least one heads)

Two notes:

As you can see in the table, experiments are not always something that we do. We can consider some to be performed by nature.
Sometimes an experiment consists of repeated trials. For example, if we flip a coin 10 times, each coin flip is a trial.

For the table above, represent each sample space as a set of numbers.

A card is randomly drawn from a deck of card consisting of the 13 spade cards. Determine the sample space, the event $E_1$ that a face card is drawn, and the event $E_2$ that a heart is drawn. (Using number to represent outcomes is optional).

A coin is flipped 3 times. Determine the sample space and the event that exactly two heads are observed.

Two dice are rolled. Determine the sample space (hint: use notation introduced here) and the event $E$ that the sum of the numbers is equal to 10. What are the sizes of $\Omega$ and $E$?

Below you can roll a pair of dice!

⚂⚄

Interpretations of probability

The probability of an event describes how likely it is for that event to occur. It can be represented as a percentage or a number in the interval $[0,1]$. For example, we may say that the probability of Heads in a coin flip experiment is 0.5 or 50%. The probability of an event $E$ is shown by $P(E)$ or $\Pr(E)$.

But what does mean when we say that the probability of an event is 𝑝? How do we relate this number to the real world? There are three interpretations of probability:

Classical: There are 𝑛 possible outcomes, where we don’t have any reason to believe one is more likely than another. If an event has probability $p$ it consists of $k$ equally likely outcomes, where $p=𝑘/𝑛$.
- Example: The probability that 5 or 6 shows when a dice is rolled is 1/3.
Frequentist: If we repeat the experiment 𝑁 times, when 𝑁 is large, and the event occurs 𝐾 times, then 𝐾/𝑁 is close to 𝑝.
- The probability of heavy traffic on I-64 at 7 am is 20%.
Subjective (Bayesian): Representing the degree of subjective belief. For example, it can help you determine how much you should bet on something.
- The probability that Lakers win NBA championship in 2021 is 40%.

The first two interpretations are commonly accepted. When we have good reason to believe all outcomes are equally probable, we can easily determine the probability of each event. Specifically, the probability of an event $E$ is $P(E)=\frac{\vert E\vert}{\vert \Omega\vert }$, where $\vert A\vert$ denotes the number of elements of $A$. This is particularly useful in games of chance, one of the first applications of probability theory. The word “fair” in expressions such a fair coin or a fair die means that the outcomes are equally likely.

If we cannot assume the outcomes are equally likely, we can collect data and using the second interpretation estimate the probabilities of events. For example, if a coin is bent and no longer fair, we can flip it 1000 times and then estimate the probability of heads. (This can be a complicated task but a close study of it is outside the scope of this course.)

The last interpretation is not accepted by everyone. The argument against it is that probability is only meaningful when it is possible to perform the experiment many times. For example, we can’t repeat the 2021 NBA playoffs many times.

Using the classical interpretation, what is the probability that a dice shows 1,2, or 3? After computing this probability, click the button below to simulate 20 dice rolls and count how many times this event occurs. Does the probability you computed match with the frequentist interpretation?

Consider the example of the pair of dice above. Using the classical interpretation of probability, and assuming all outcomes are equally likely, what is the probability of the sum of the dice being 10?

Sets … again

Let’s review a few set operators, which will be useful for us:

The union of sets $E_1,E_2,\dotsc$ is the set of elements included in any of the individual sets.
The intersection of sets $E_1, E_2,\dotsc$ is the set of elements included in all of the individual sets.
The sets $𝐸_1,𝐸_2,…$ are disjoint if the intersection of any two of them is the empty set.
- In probability theory, a collection of disjoint events is called mutually exclusive.
The difference between a pair of sets $E_1 \setminus E_2$ is the set of elements included in $E_1$ but not in $E_2$.

The union and intersection operators satisfy a number of properties:

Commutativity and associativity
- $A\cup B = B\cup A,\qquad\qquad\qquad A\cap B = B\cap A$
- $A\cup (B\cup C) = (A\cup B)\cup C,\qquad A\cap (B\cap C) = (A\cap B)\cap C$
Distributive property
- $A\cup (B\cap C) = (A\cup B)\cap (A\cup C)$
- $A\cap (B\cup C) = (A\cap B)\cup (A\cap C)$

Axioms of probability

Like other branches of mathematics, to build probability theory, we need definitions and axioms. There are three important axioms of probability, developed by Kolmogorov:

The probability of an event is a nonnegative real number.
The probability of the sample space $P(Ω) = 1.$
(The sum rule for probability) For a countable collection of events $𝐸_1,𝐸_2,…$ that are mutually exclusive

\[𝑃(E_1\cup E_2\cup \dotsm \cup E_n)=\sum_{i=1}^n 𝑃(𝐸_i).\]

The axioms are valid, regardless of the interpretation of probability that we are working with. In particular, note that they are compatible with the classical interpretation. For example, consider the probability of the event $E$ that an even number shows when a die is rolled. By the classical interpretation, we have $E=\{2,4,6\}$ so $P(E) = \frac36$. By the third axiom, $P(E) = P(\{2\})+P(\{4\})+P(\{6\}) = \frac16+\frac16+\frac16=\frac36$.

Probabilities of sets

The probability space describes the collection of sets (events) that are assigned probabilities. From the axioms of probability, there are some important consequences for sets:

Complementary events: $P(E^c)=1-P(E)$.
- Proof: Since $𝐸$ and $𝐸^𝑐$ are mutually exclusive, and their union is the sample space $\Omega$, $P(E)+P(E^c)=P(E\cup E^c)=P(\Omega)=1$.
$0\le P(E)\le 1$.
- Proof: From the first axiom, $P(E)\ge 0$. Also, $P(E) = 1-P(E^c)\le 1$.
The empty set: $P(\varnothing) = 0$ since $\varnothing^c=\Omega$.

A fair coin is flipped three times. What is the probability that at least one heads is observed.

The probability of any union of disjoint events can be described by the third axiom. How about the intersection of a pair of events? We can prove that $𝐸_1\cap 𝐸_2$ and $𝐸_1\setminus E_2$ are mutually exclusive and combine to form $E_1$. Thus,

$𝑃(𝐸_1∩𝐸_2 )+𝑃(𝐸_1\setminus 𝐸_2 )=𝑃(𝐸_1 )$.

Finally, what about the probability of the union of two events when they are not disjoint?

Prove the following two equalities: \begin{align*} P(E_1\cup E_2) &= P(E_1\setminus E_2) + P(E_1 \cap E_2) + P(E_2\setminus E_1),\\ P(E_1\cup E_2) &= P(E_1) + P(E_2) - P(E_1 \cap E_2). \end{align*}

A random two-digit natural number is chosen (all numbers from 10 to 99 have equal probabilities). What is the probability that the number is a multiple of 2 or 3 (or both)? Simulate choosing 30 random numbers by clicking the button below. How does the empirical result compare to the value you computed?

Write a question that you still have about the material above.

Counting

Recall that when all outcomes are equally likely,

\[P(E) = \frac{|A|}{|\Omega|}\]

So to find probabilities, we need to be able to count the outcomes in a given event and the total number of possible outcomes. Sometimes this counting is straightforward and sometimes we need to use counting techniques. Here are some examples:

How many cards are “hearts” in a standard deck?
How many ways can we roll a pair of dice to add up to 7?
How many three-digit numbers are there with the digits 5,6,7?
How many binary sequences of length 8 are there with exactly three 1s?
How many possible three-person teams are there among students in this class?

Counting rules

We have already seen the rule of sum and the rule of product. In particular, the rule of product says:

“If action 1 can be done in $m$ ways, action 2 can be done in $n$ ways, and actions 1 and 2 must be both performed, then there are a total of $m\times n$ ways to perform them.”

We can extend the rule of product to multiple actions. We have used this to show that there are $2^N$ binary sequences of length $N$. Let’s review via an example: How many binary sequences of length 8 are there? We have two ways to choose the first bit (either 1 or 0), 2 ways to choose the second bit, and so on. So we have

\[\underbrace{2\times2\times\dotsm\times2}_{8\ times} = 2^8 = 256\]

binary sequences of length 8.

We now add two new rules that follow from the rule of product: counting permutations and combinations. A permutation is an arrangement of a set of objects in a row. A combination is a selection of a number of objects from a bigger set without regard to order.

Counting permutations: The number of ways $n$ objects can be arranged in a row is $$n!=1\times2\times\dotsm\times n.$$

⭐ Counting combinations: The number of ways $k$ items can be chosen from a set of $n$ items is denoted ${n\choose k}$ and read $n$ choose $k$. We have $${n\choose k}=\frac {n!}{k!(n-k)!}.$$

Aside: ${n\choose k}$ is called a binomial coefficient, because of the binomial theorem.

We’re not going to prove these. Instead, let’s see two examples. In these examples the numbers are small enough that we can check our answers by listing all the possibilities.

In how many ways can we write a 3-digit number using digits 5,6,7? We have to arrange these three digits in a row, which we can do in $3!=1\times 2\times 3 = 6$ ways. The numbers are $567,576,657,675,756,765$.
In how many ways can we choose two people from the set {Alice, Bob, Charlie, Dave, Eve}? The answer is ${5\choose2}=\frac{5!}{2!3!}=\frac{120}{12}=10.$ The possibilities are AB, AC, AD, AE, BC, BD, BE, CD, CE, DE (using their initials)

How many 8-bit binary sequences are there with exactly three 1s? If we choose an 8-bit binary number at random, what is the probability that it has three 1s?

Permutations

Here are the number of permutations for small values of $n$.

$n$	0	1	2	3	4	5	6	7	8	9	10
$n!$	1	1	2	6	24	120	720	5040	40320	362880	3628800

You can see that the number of permutations grows very quickly.

We randomly shuffle six cards numbered from 1 to 6. What is the probability that they are in order?

Now let’s do the same exercise for a full deck of cards. What is the probability that a deck of 52 cards is in order after a random shuffle? An incredibly small number: $1/52!= 1.24×10^{−68}.$

Just for fun: How large is 52! ?

\[52! = 80658175170943878571660636856403766975289505440883277824000000000000=8.066×10^{67}\]

This is very very large! If everyone who has ever lived shuffled a deck once every second since the beginning of time, the probability that there are two identical decks (with the same order) is

\[\le \frac{(10^{11}×4.32×10^{17})^2}{8.066×10^{67}}=2.31×10^{−11}\]

(We are not going to prove this, but you may be able to guess where each number comes from) We can be pretty sure that no two randomly shuffled decks will have the same order because the number of possibilities is so large. If you hold a shuffled deck of cards in your hands, you can confidently say that that particular arrangement has never happened before.

How many bits do we need to represent the order of a deck of cards?

Method 1: If you want to represent each card separately, you need 6 bits / card and there are 52 cards so you need 6 bits/card × 52 cards = 312 bits.
Method 2: Alternatively, you can look at the problem as identifying one permutation among 52! possibilities. So you need $\log_2(⁡52!)=225.58$ bits.

The first method is simpler while the latter is more space-efficient (i.e., uses less memory). In any case, despite the large number of possibilities, you need a relatively small number of bits to represent a particular outcome.

Combinations

Combinations are important in probability because they allow us to answer questions such as:

When playing dart, Alice can hit the bullseye with probability 1%. What is the probability that she hits the bullseye twice in 10 throws?
Each bit stored on a flash drive flips with probability $10^{-6}$ due to random noise. If I store $10^9$ bits of information on it, what is the probability that there are more than 10 bit flips?

But before getting there, let us discuss a couple of properties of the number of combinations.

Suppose we want to pick three people from the set {Alice, Bob, Charlie, Dave, Eve}. In how many ways can we do so?

We can see that the answer is the same as in choosing 2 people, which is ${5 \choose 2} = 10$. Is this a coincidence? No. The number of ways we can choose $k$ items out of $n$ items is the same as the number of ways we can choose $n-k$ items out of $n$ items. For example, if you have $n$ friends but you can only invite $k$ of them to your birthday party, you can either choose which $k$ friends to invite or which $n-k$ friends not to invite. (Depending on the type of person you are, one way of deciding is more fun than the other.) In summary:

\[{n\choose k}={n\choose n-k}.\]

Note that we didn’t use the formula for ${n\choose k}$ to arrive at this conclusion.

Suppose we want to pick three people from the set {Alice, Bob, Charlie, Dave, Eve}.

In how many ways can we do so if we have to pick Alice? (compute this without first computing the total number of possibilities)
In how many ways can we do so without picking Alice? (compute this without first computing the total number of possibilities)
What is the total number of possibilities?

In the previous exercise, since we either pick Alice or we don’t, the total number of possibilities is equal to the number of possibilities in which Alice is chosen plus the number of possibilities in which Alice is not chosen, which is verified by noting that

\[{5\choose 3}={4\choose 2}+{4\choose 3}.\]

Using the same argument, we can show that in general:

\[{n\choose k}={n-1\choose k-1}+{n-1\choose k}.\]

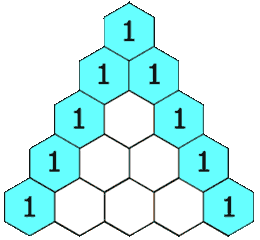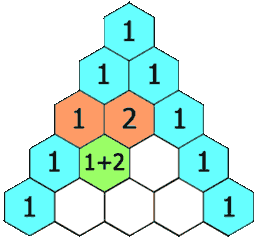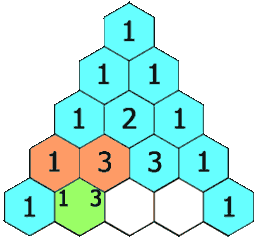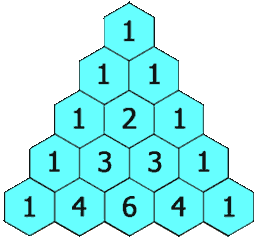
If your friends are {Alice, Bob, Charlie, Dave, Eve, Frank} and you pick three at random to invite to your party (so that those left out are not upset!), what is the probability that Alice is invited?

The expression above provides a way to compute ${n\choose k}$ recursively. In particular, Pascal’s triangle, which is a triangular table whose $n$th row is ${n\choose 0},{n\choose1},\dotsc,{n\choose k},\dotsc,{n\choose n}$ can be constructed this way:

\begin{equation*} \begin{array}{rccccccccccc} & & & & & 0 \choose 0\\ & & & & 1 \choose 0 & & 1 \choose 1\\ & & & 2 \choose 0 & & 2 \choose 1 & & 2 \choose 2\\ & & 3 \choose 0 & & 3 \choose 1 & & 3 \choose 2 & & 3 \choose 3\\ & 4 \choose 0 & & 4 \choose 1 & & 4 \choose 2 & & 4 \choose 3 & & 4 \choose 4\\ \end{array} \end{equation*}

Each element can be found as the sum of the two elements above it. For example, ${3\choose2} = {2\choose1}+{2\choose2}$. You can see this construction on the left (image from Wikipedia) and the triangle for $n=0,\dotsc,5$ on the right.

\begin{equation*} \begin{array}{rccccccccccc} n=0& & & & & & 1\\ n=1& & & & & 1 & & 1\\ n=2& & & & 1 & & 2 & & 1\\ n=3& & & 1 & & 3 & & 3 & & 1\\ n=4& & 1 & & 4 & & 6 & & 4 & & 1\\ n=5& 1 & & 5 & & 10 & & 10 & & 5 & & 1\\ \end{array} \end{equation*}

Write a question that you still have about the material in this section.

Experiment	Sample space	Example events
Cloud cover tomorrow	clear [0], mostly clear [1], partly cloudy [2], mostly cloudy [3], cloudy [4]	\(\{0,1,2\}\) (a decent amount of sunshine)
A dice is rolled	1,2,3,4,5,6	\(\{2,3,5\}\) (a prime number showing)
Sun goes supernova in the next 24 hrs	it does [1], it doesn’t [0]	\(\{0,1\}\) (all possible outcomes)
A coin is flipped twice	two heads [(0,0)], heads then tails [(0,1)], tails then heads [(1,0)], two tails [(1,1)]	\(\{(0,0),(0,1),(1,0)\}\) (at least one heads)