Sampling signals

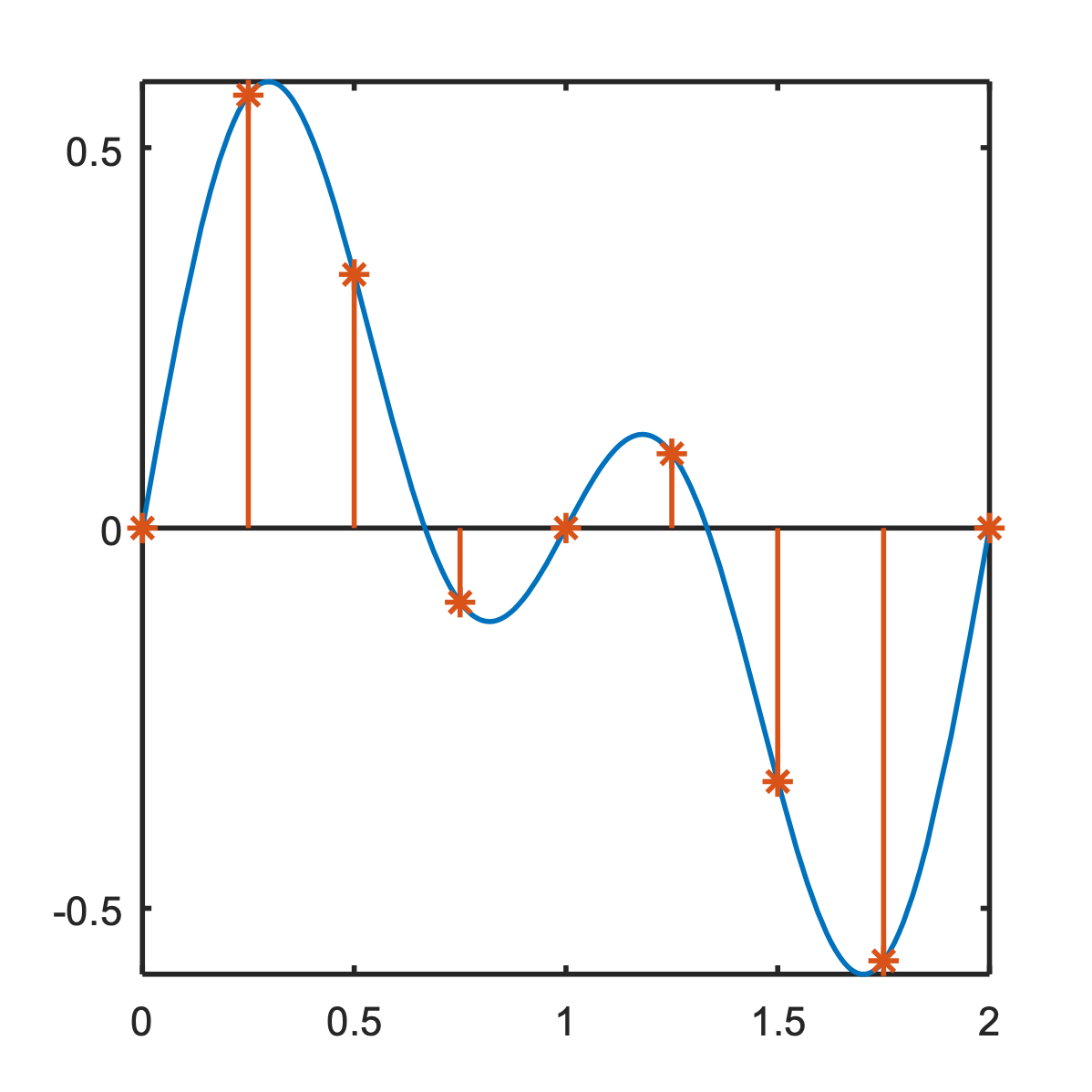
Information in the real world is analog. To store them on a computer, we sample the signal:

Original Signal	Sampling	Sampled and Quantized

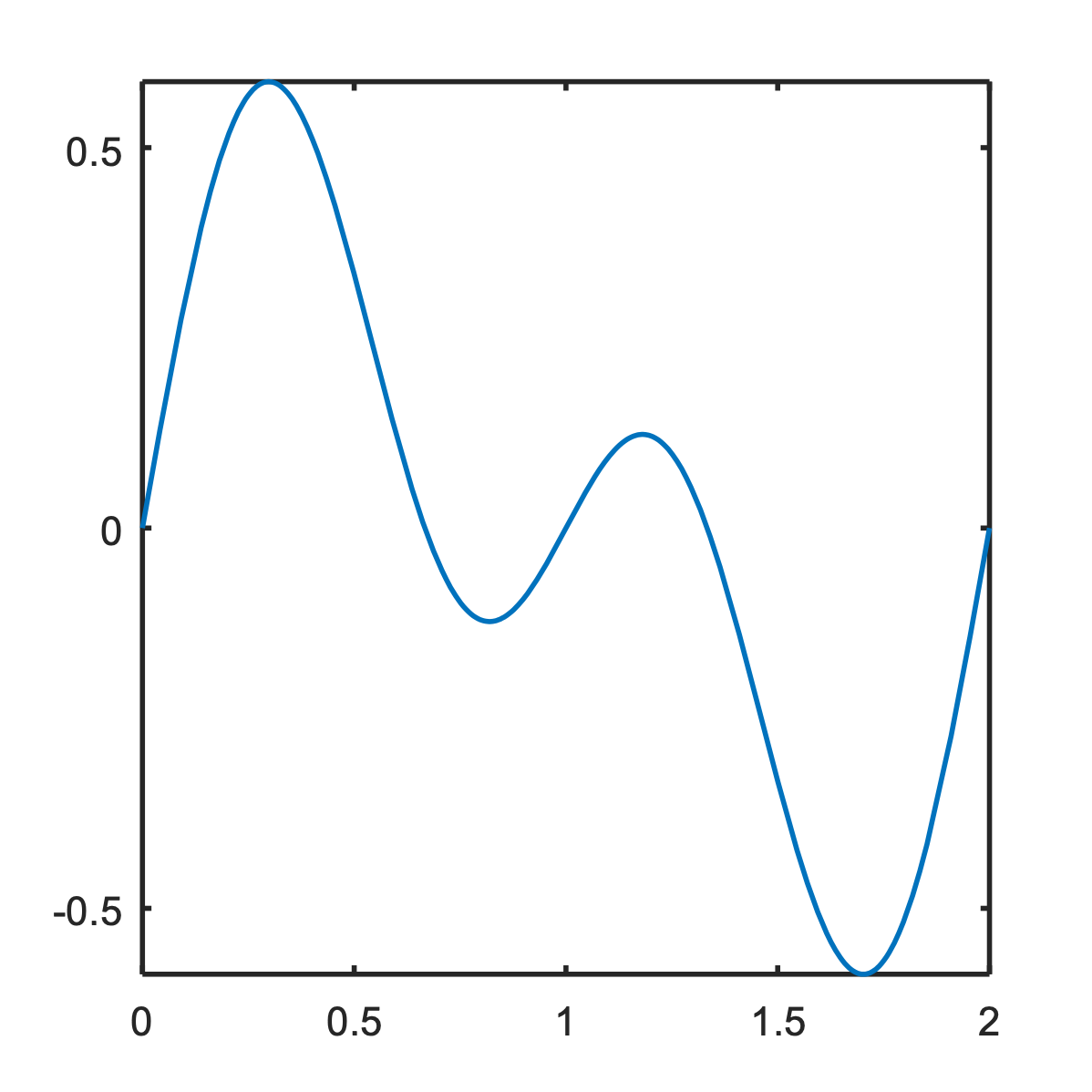
Reconstruction But how can recover the original signal? There are many analog signals (an infinite number, actually) that fit these samples:

Possible Reconstruction 1	Possible Reconstruction 2

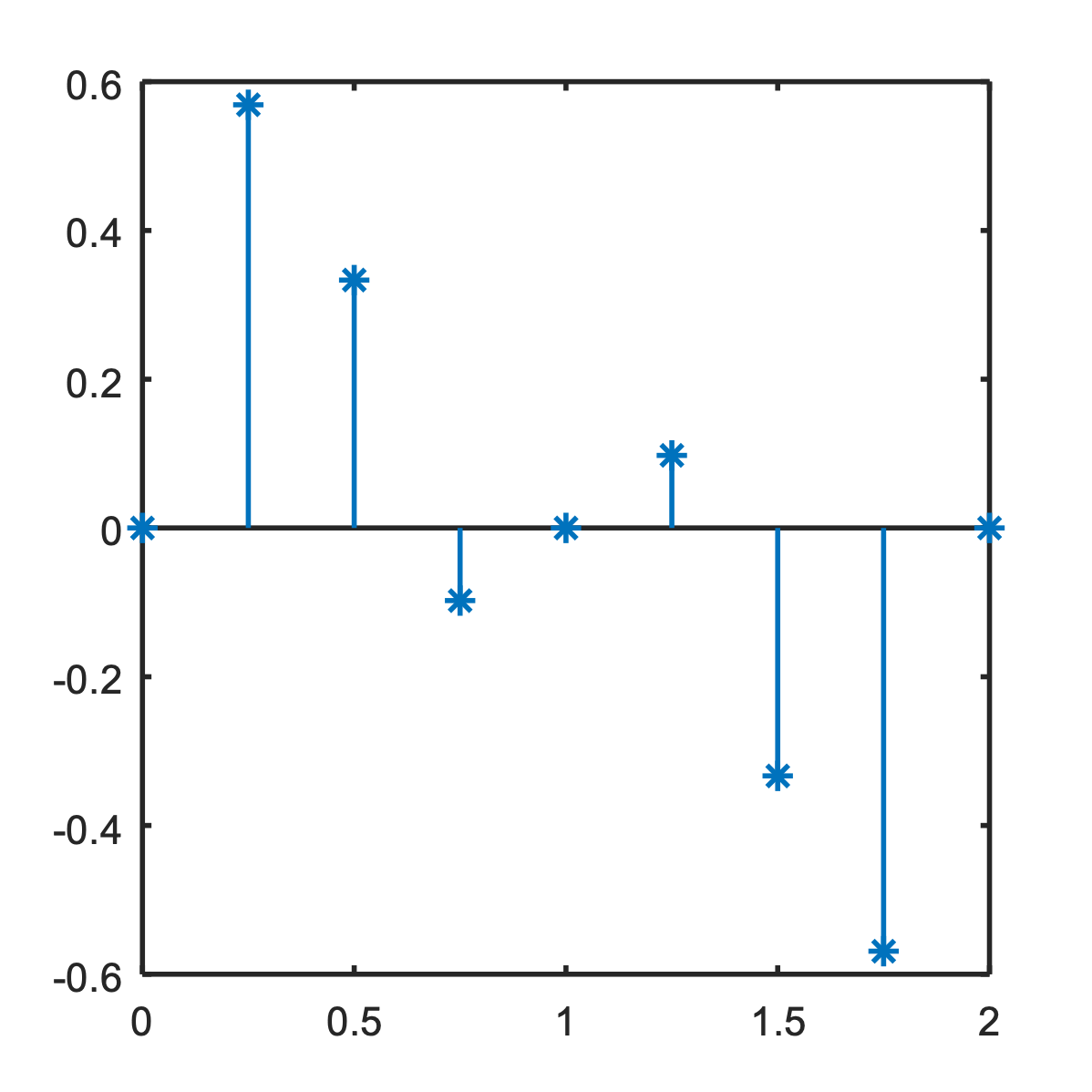
Only sampled (and quantized) values are stored

Sampling and the spectrum

We know that any signal can be viewed as a weighted sum (integral) of complex exponentials. So let’s first consider sampling a complex exponential. A complex exponential is defined by its magnitude, frequency, and initial phase like: $Ae^{i (2\pi ft + \phi)}$. So the goal is to find these quantities from samples. For simplicity, we will assume that $A = 1$ and $\phi = 0$. Let’s see under what conditions we can recover $f$ from samples

Sampling complex exponentials

The animation on the left is a sampled exponential at the rate of three samples per second (time is slowed by a factor of 12). In the middle, the animation shows the sampled signal at each interval.

Original Signal (slowed 12x)	Sampled Signal (slowed 12x)	Sampled Signal (real time)

Let’s overlap these to make sure the samples agree with the original signal. The samples are taken at 0s, $\frac13$s, $\frac23$s,$\ldots$. Is there any other frequency that would result in the same samples?

• At time $\frac13$, the sample is at $\frac13$ of the cycle. So $f = {\frac13}/{\frac13} = 1 Hz$
• But as we don’t see what happens between $t = 0$ and $ t = \frac13$, the real signal may also have traveled $\frac43$ of a cycle. So it is possible that $f = \frac43/\frac13 = 4 Hz$.
• Also possible: $f = \frac{-2}3/\frac13 = -2 Hz$.
• All possibilities: $1, 4, 7, 10, \ldots Hz$ and $−2, −5, −8, \ldots Hz$.

Bandwidth and sampling

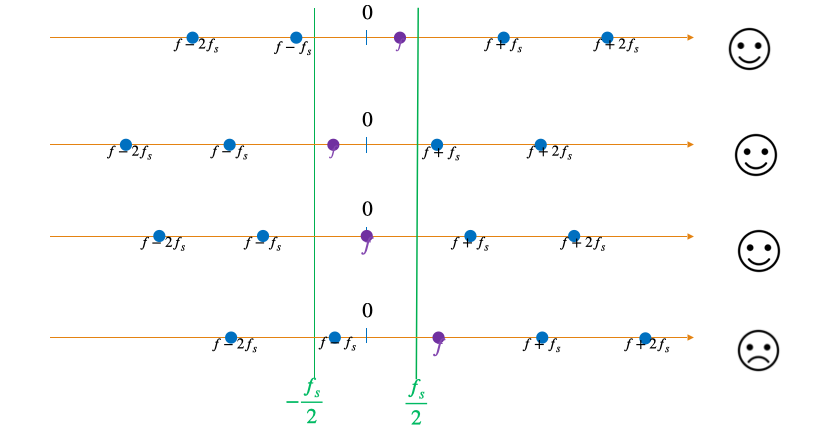
If we sample with frequency $f_{s}$ signals with the following frequencies appear the same

$f,f \pm f_{s},f \pm 2f_{s},\ldots$

How can we ensure that we can recover the correct frequency? Not possible if we don’t make any additional assumption about the range of possible frequencies

If the true frequency $f$ satisfies $- \frac{f_{s}}{2} < f < \frac{f_{s}}{2}$, then it can be recovered correctly.

Bandlimited signals

So the true frequency must be restricted in a certain sense. But how can we ensure this is the case?

Fortunately, real signals are band-limited, i.e., there is a number $B$ such that all their frequency content is between $- B$ and $B$

An analog (continuous-time) signal that has a finite range of nonzero frequency content is called bandlimited.

If our bandlimited signal has content up to positive frequency B, we call B the bandwidth of the signal. The signal’s frequency content spans $[-B, B]$

Suppose our signal is a sinusoid: $x(t) = 2cos(2π(500)t + π/4)$.

What does the analog spectrum look like?

What is the bandwidth of this signal?

Let’s make our observations precise.

If for $f$ in the range $[-B,B]$, to recover it without ambiguity:

$f \pm f_{s}$must fall outside the range $\lbrack - B,B\rbrack$ that is, $f + f_{s} > B$ and $f - f_{s} < - B$

Example: If $f_{s} = 3$, what is the largest value for $B$?

So what is the relationship between $f_{s}$ and $B$ for correct recovery?

The largest frequency is $B$. We need $B + f_{s} > B$ (obvious) and $B - f_{s} < - B \Rightarrow f_{s} > 2B$

The smallest frequency is $- B$. We need $- B + f_{s} > B \Rightarrow f_{s} > 2B$ and $- B - f_{s} < - B$ (obvious)

So we need $f_{s} > 2B$.

The sampling theorem

If $2B < f_{s}$ then given samples from a complex exponential with frequency $f$in the range $\lbrack - B,B\rbrack$, we can correctly recover $f$

The same holds for a combination of complex exponentials if all their frequencies are in the range $\lbrack - B,B\rbrack$, and so for all bandlimited signal with bandwidth $B$

The bandwidth of human voice (speaking) is 4kHz. At quantization bit depth of 8 bits/sample, what data rate is needed to transmit human voice?

$f_{s} = 8kHz,Rate = 8000\frac{samples}{second} \times 8\frac{bits}{sample} = 64000\frac{bits}{second} = 64kbps$

This is what happens on your phone

In the old modems it was the opposite. Data was converted to analog signal with bandwidth of 4kHz, since phone circuits could carry analog signals with bandwidth of 4kHz

But why were modems 56kbps instead of 64kpbs? One out of each 8 bits was used for control purposes when transmitting data